本讲为开学第一课的内容, 主要作热身之用. 我们不会引入很多新概念,
绝大多数概念你都应该在之前的微观经济学和博弈论中学过.
教师默认你熟悉以下知识:
- 离散型概率分布,
- 离散型随机变量的期望,
- 确定情形下的偏好理论.
不确定情形下的决策
我们将研究张三在不确定情形下的决策问题.
- 一般称张三为决策者 (DM, Decision
Maker)
- 这里的张三是一个泛指. 有时, 他是一个学生或投资者; 有时,
他也可以是一个企业或国家.
在信息不确定性时, 张三的每个决策所导致的结果是随机的, 而非确定的.
- 是否应该购买英伟达公司的股票? 如果选择购买,
其投资回报是不确定的.
- 是否应该努力学习信息经济学? 如果选择学习, 其回报也是不确定的,
并且在这门课上的(过度)投入会挤出你学习其它课程或睡觉的时间.
我们需要有一个模型来描述张三在面对不确定性时如何做出选择.
市场中的不确定性
- 俄罗斯 2022 年 2 月入侵乌克兰, 当天全球股票市场开盘跌 3.5%
- 然而, 当天收盘时却涨了 0.4% (我买的一支场内交易基金甚至涨了
3.8%)
问: 我们该如何描述这种不确定性?
答: 使用概率的工具来描述
- 方法一: 直接将不确定性描述为所有可能结果的概率分布
经济学中, 一般把这种概率分布称为彩票 (lottery),
我们可以用树形图来表示彩票,
下面是两个关于彩票的图例.
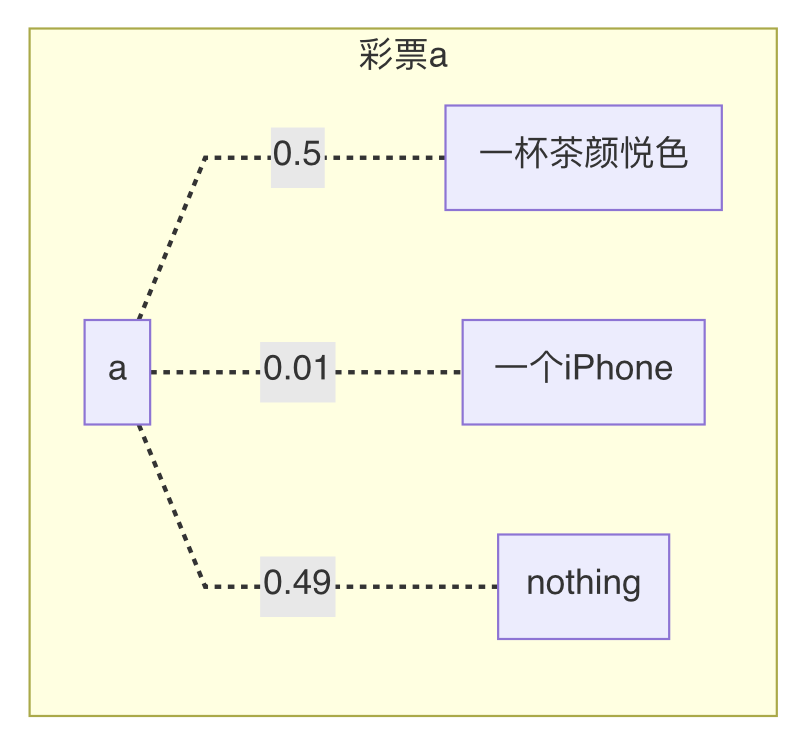
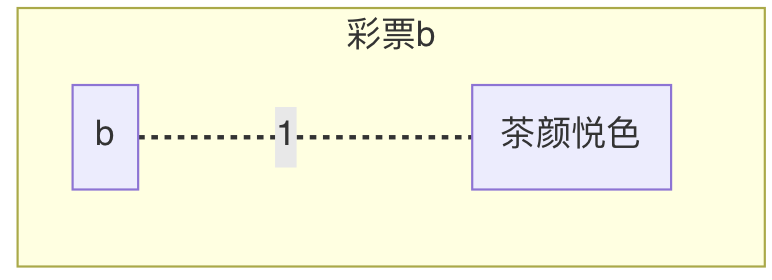
另一种表示彩票的记号:
- 彩票 a= (0.5 \circ \text{茶颜悦色}, 0.01
\circ \text{iPhone},
0.49 \circ \text{nothing})
- 彩票 b= (1 \circ
\text{茶颜悦色})
客观概率
我们前面使用的方法一, 适合用来描述客观概率的情形.
\text{彩票 = 所有可能结果上的概率分布}
- 比如投掷一枚公平硬币: 1/2概率正面朝上获得一元,
1/2概率反面朝上亏损一元.
- 这个概率是"客观"的, 绝大多数人都会同意这个概率分布
- 但是, 几乎所有涉及到真实市场的信息不确定,
都不能用客观概率描述
- 例: 俄罗斯入侵乌克兰后, 当天股票市场大盘变动的概率分布是?
主观概率模型:
最终收益由状态 (state) 决定

问: 我们如何给每个分支结果分配一个概率?
- 没有统一答案.
- 现实中关于足球比赛的赌局很多. 这类赌局之所以存在,
就是因为人们对哪支球队能获胜持不同判断.
对于这类"主观概率"情形, 我们一般建立如下模型:
Step 1: 确定所有可能状态构成的集合
- 对于前面的世界杯彩票的例子, 它的状态空间是:
{ 巴西夺冠, 德国夺冠, . . . , 新西兰夺冠 }
Step 2:
将赌局描述为状态空间到最终收益的映射
- 西班牙夺冠 \mapsto -\$100, 法国夺冠
\mapsto -\$100,...
- 巴西夺冠 \mapsto +\$100, 阿根廷夺冠
\mapsto +\$100,...
- 喀麦隆夺冠 \mapsto \$0, 澳洲夺冠
\mapsto \$0, 日本夺冠 \mapsto \$0, ...
Step 3: 给状态空间中的每一个状态赋予一个主观概率
- p(巴西夺冠) = p(西班牙) = 0.1
- p(日本夺冠) = 0.02, p(中国夺冠) = 0
- ...
当你完成上述三个步骤后, 最后也可以得到一个描述赌局的彩票 p:
- 例: p = (0.5 \circ -$100, 0.45 \circ $100, 0.05 \circ $0). 这里的概率仅表示张三的判断,
你很可能和张三的判断不一致.
状态空间和信念
上述步骤中, 最复杂的应该是第一步和第三步.
- 第一步需要确定状态空间 Ω, 即所有可能状态构成的集合.
- 第三步需要确定状态空间上的概率分布
- 这里的概率是主观概率,
因为不同的决策者很可能持有不同的信念.
- 尽管我们无法观测到每个人脑海中的真实想法, 但我们可以观测到具体行动.
现实的赌局中, 有人会买西班牙队夺冠, 有人会买阿根廷夺冠,
这说明他们决策模型中的主观概率不同.
期望效用模型
无论是主观还是客观概率, 我们最后都会用期望效用 (expected utility)
模型来描述张三的决策.
- 张三给彩票的每个可能结果赋予一个数
- 张三对彩票的所有可能结果进行概率评估 (objective or subjective),
然后计算彩票的期望效用
- 张三选择期望效用最高的彩票 (若期望效用最高的彩票不唯一,
选择其中任何一张彩票对张三而言都是最优的,
张三也可以在这些最优的彩票之间随机)
小结
本讲简单介绍了期望效用模型.
张三在期望效用模型下的具体决策流程如下:
- 确定自己关于确定性结果的的效用函数 u;
- 如果该情形涉及到主观概率, 张三还要确定状态空间和状态的概率分布 p;
- 计算期望效用, 并选择期望效用最高的彩票
绝大多数经济学模型中,
参与人的决策行为都符合我们上面描述的期望效用模型. 这时,
期望效用模型是否"合理"就成了一个关键问题. 我们之后介绍的 vNM 公理化模型,
为客观概率下期望效用模型的合理性提供了依据. 对于主观概率的情况, 一般用
Savage 公理化模型来论证其合理性. Savage 模型的描述有点复杂,
本课程略过不谈, 你们将来如果要读研究生应该会专门学习 Savage 模型.
很多经济学入门书中, 常常会提到我们模型中的参与人都是"理性"的.
随着你对经济学学习的逐渐深入,
你会越来越少接触到"理性的"或"理性人"这种模糊的说法.
- 我希望同学们在这门课中, 不要使用"理性人"这个外行词.
你需要明确说明张三在不确定情形下的具体决策流程, 比如期望效用模型.
如果这个模型的结果与现实或实验结果不一致,
你应该反思张三的决策环节和我们的模型假设, 找出可能存在的问题.
- 如果你对这个问题感兴趣, 甚至可以进一步思考如何推广我们的决策模型,
使其与现实观察相符; 而不是直接懒惰地给出最终结论: 张三是不理性的.
练习: Ellsberg 悖论
这个练习的目的在于介绍 Ellsberg 悖论, 它是经济学中最著名的实验(之一).
本练习包含四小问, 前三问只要看懂题目即可作答,
不需要用到任何经济学专业知识.
实验设计如下: 有两个密封的盒子, 分别记作 A 和 B. 已知
- 盒子 A 中装有 100 个红球和 100个黄球
- 盒子 B 中装有 200 个红球和黄球 (红, 黄球数量不确定)
比较如下两个赌局:
- 赌局1: 从盒子 A 中随机抽一个球, 若抽到红球, 奖 100; 否则无奖励
- 赌局2: 从盒子 B 中随机抽一个球, 若抽到红球, 奖 100; 否则无奖励
第一问: 你更愿意参加赌局1还是赌局2, 或者无差异?
再比较如下两个赌局
- 赌局3: 从盒子 A 中随机抽一个球, 若抽到黄球, 奖 100; 否则无奖励
- 赌局4: 从盒子 B 中随机抽一个球, 若抽到黄球, 奖 100; 否则无奖励
第二问: 你更愿意参加赌局3还是赌局4, 或者无差异?
在真实的经济学实验中, 绝大多数人都同时认为
- 赌局1 严格优于赌局2,
- 赌局3 严格优于赌局4.
第三问: 解释实验结果, 即为什么大多数人会认为赌局1
优于赌局2, 而赌局3 优于赌局4. (注: 你不需要给出专业的"心理学"解释,
试着代入没有学过期望效用模型的普通人视角回答即可.)
第四问: 实验结果可以由期望效用模型解释么?




